- 単回帰分析の使いどころ
- 相関がある値から予測を立てる方法
コールセンターで単回帰分析する場面例

ゆうたろうくん、
一日の応答件数目標22件、達成が厳しそうだね。

はい…。22件達成が微妙です。
後処理と応答数で相関があるので、
今は後処理短縮に力を入れてます。

そうか。
後処理と応答数の相関が高いんだね。
ちなみに、後処理がどれくらいだと応答件数の目標達成できそう?

えっとー・・・。
そこまでは見てませんでした。
もう一度確認してみます!
上記のやり取りで例えば、
「後処理4分半以内なら、目標達成できます」
とか言えると、かっこいいですよね。
回帰分析なら言えるんだ
今回は、コールセンターでの予測を立てるため、相関関係にある2つの値から、
応答件数22件の時、後処理が〇分だ
こんな予測が立てられる「回帰分析」をお伝えしていきます。
相関については過去記事でチェック!
相関関係というのは
コールセンター管理者の仮説検証【相関係数】
「一方が増加する時、他方が増加する
もしくは減少する傾向が認められるという二つの量の関係」を言います。
もし相関係数について詳しく振り返りたい場合は、以下の記事をご確認ください。
» 参考:仮説検証!コールセンター管理者の分析スキル【相関係数】
それでは、二つの相関が高い値から「一方が〇〇の時、もう一方は〇〇だ」と予測が立てられる「単回帰分析」の説明をしていきます。

- コールセンター暦15年以上
- 元外資系メーカー営業マン
- 受信/発信/講師/SV/Mgr経験
- 高度HSPの繊細さん
- 在宅コールセンター副業経験有
- コールセンターハック管理人
コールセンターで予測を立てるには単回帰分析を使う!


相関までチェックしてるなら
単回帰分析するといいよ。

単回帰分析?
難しそうですね。。。

Excelですぐに計算できるから
手順を教えるね!
一方が〇〇の時、もう一方は〇〇だ
これを説明することが、単回帰分析をする目的です。
今回の例で言うと、こうです。
「応答件数〇件の時、後処理が〇〇分だ」
この記事から離脱されてしまう心配を覚悟で、まず計算方法の結論から書きます。
回帰分析の計算式とは?回帰分析とは?
y:目的変数 = (a:切片 × X:説明変数)+b:傾き
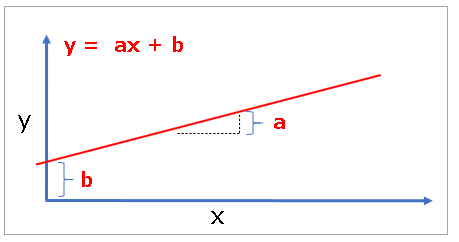
回帰分析(かいきぶんせき)とは、回帰により分析する事。
Wiki
回帰で使われる、最も基本的なモデルは Y=AX+Bという形式の線形回帰である。
「あぁ画面閉じよう」と思った方、お待ちください
簡単に計算できてしまうのでご安心を。
実際、私も詳しい所まで理解していません。
Excelを使えば、式や仕組みを理解していなくてもOKです。
実例!Excelで簡単に計算しちゃおう
やり方は以下画像の赤く囲った①と②の二通りを紹介します。
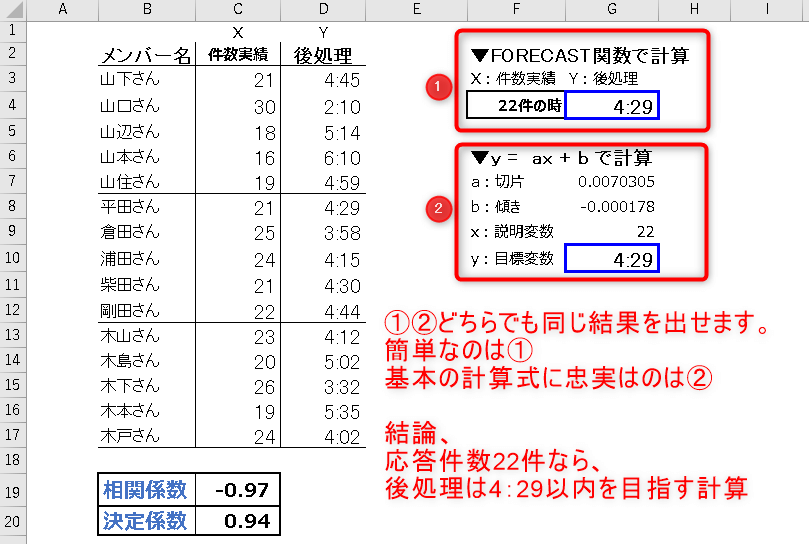
ちなみに以下計算式を今回の例にあてると、
y:目的変数 = (a:切片 × X:説明変数)+b:傾き
y = 後処理
x = 応答件数
「a:切片」「b:傾き」は、計算中に出る値となってきます。

もう、取り合えずやり方だけ教えて。
簡単に予測計算!ExcelのFORECAST関数を使う


じゃあ具体的に
Excelでの出し方を説明するね!

はい!
お願いします!
では、コールセンターでの予測を立てる具体的な計算方法の説明です。
こちらは、Excelの関数を一つだけ使ってすぐに計算できる方法。
理屈を理解せずに、すぐ答えが出せるおススメのやり方です。
後処理の予測を単回帰分析で出してみよう!
- STEP1
C列に応答件数、D列に後処理が並んだ表を用意します。
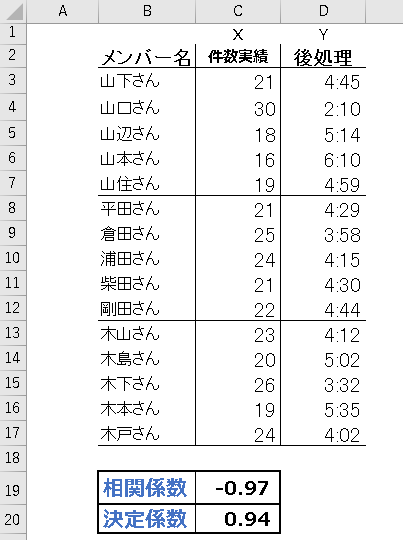
- STEP2
F4に応答目標の「22」を入力し、隣のG4列をあけておきます。
※画像上「22件の時」という表記になるよう書式設定しています
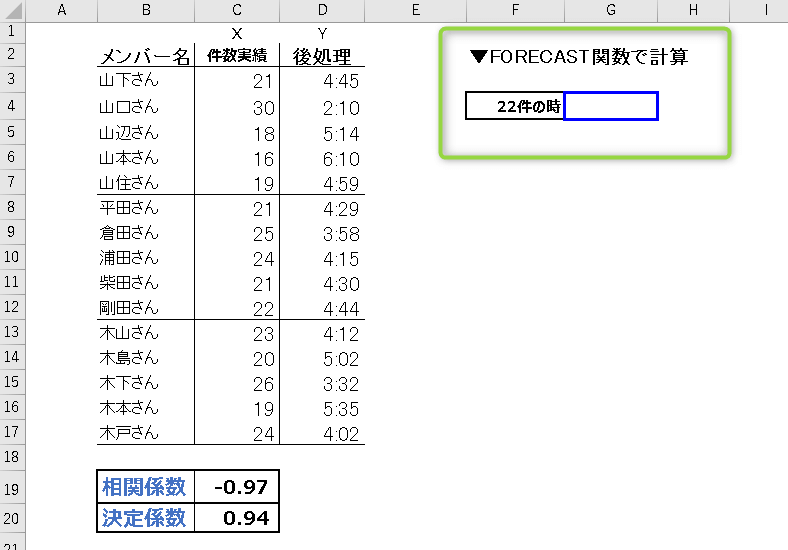
- STEP3
G4のセルに、以下を入力します。
=FORECAST(F4,D3:D17,C3:C17)
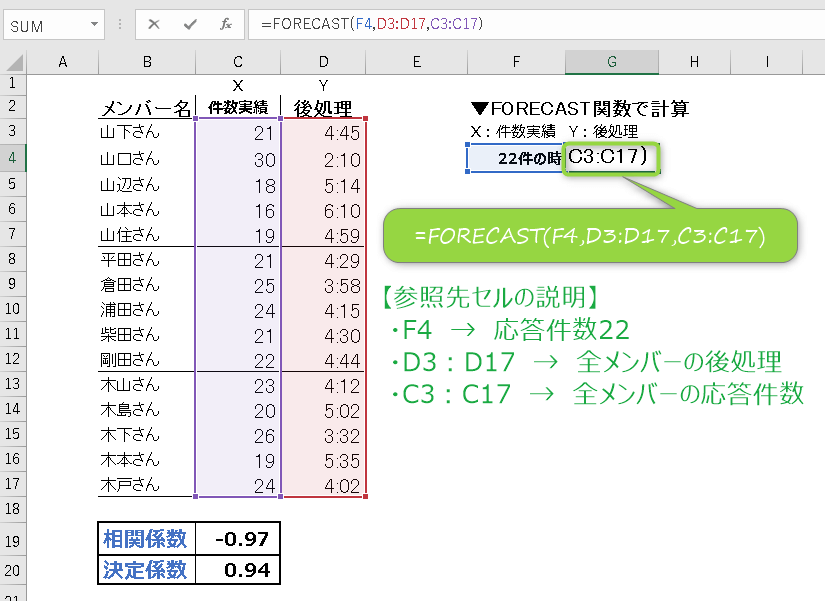
- STEP4
G4セルに「4:29」と出ました。

- STEP5
この結果、以下であると言えます。
「応答件数22件の時、後処理が4:29だ」
以上
上記の例でいうと相関係数も-0.97と「-1」に近く、決定係数も「1」に近いので、ほぼ正確と言える答えだと言えます。
※決定係数
回帰式が正しいか判断できる数字
0.5以上で精度が高いと判断できます。
Excelで回帰式に忠実に予測を計算する


覚えなくてもいいけど
回帰式に忠実に
Excelで計算する方法も補足するね。

はい!
内容を理解するのに
良いかもですね。
y:目的変数 = (a:切片 × X:説明変数)+b:傾き
この計算式にしっかり数値をあてはめながら計算する方法です。
計算式にあてはめて後処理を単回帰分析してみよう
- STEP1
C列に応答件数、D列に後処理が並んだ表を用意します。
F列とG列にそれぞれ計算式中の値が入るようにしていきます。
最終的に青枠の目標変数が計算できればゴールになります。
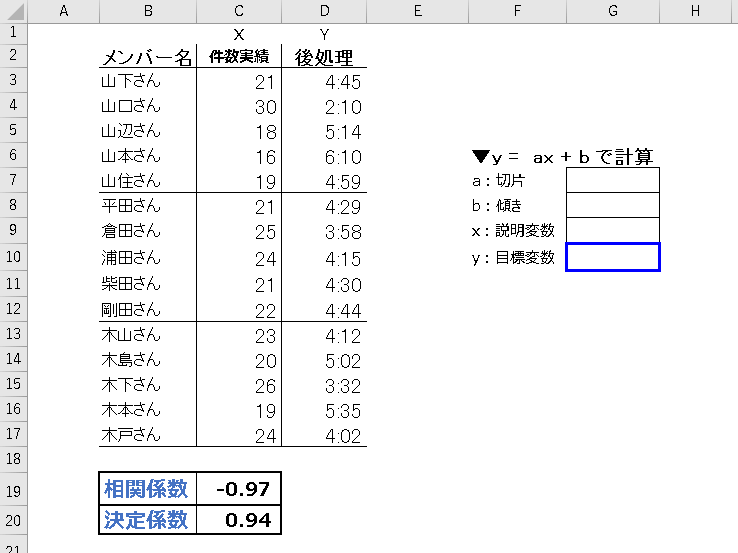
- STEP2
セルG7のa:切片を求めます。
=INTERCEPT(D3:D17,C3:C17)
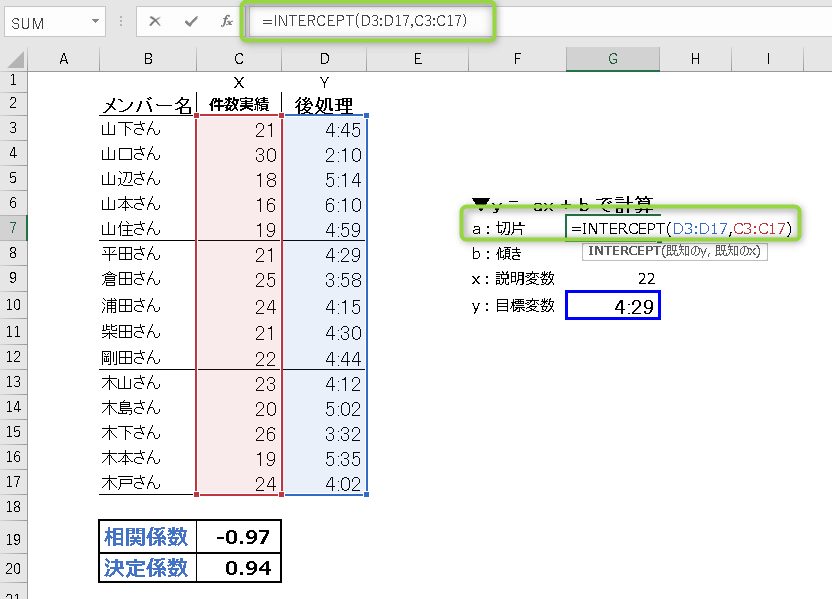
- STEP3
セルG8のb:傾きを求めます。
=SLOPE(D3:D17,C3:C17)
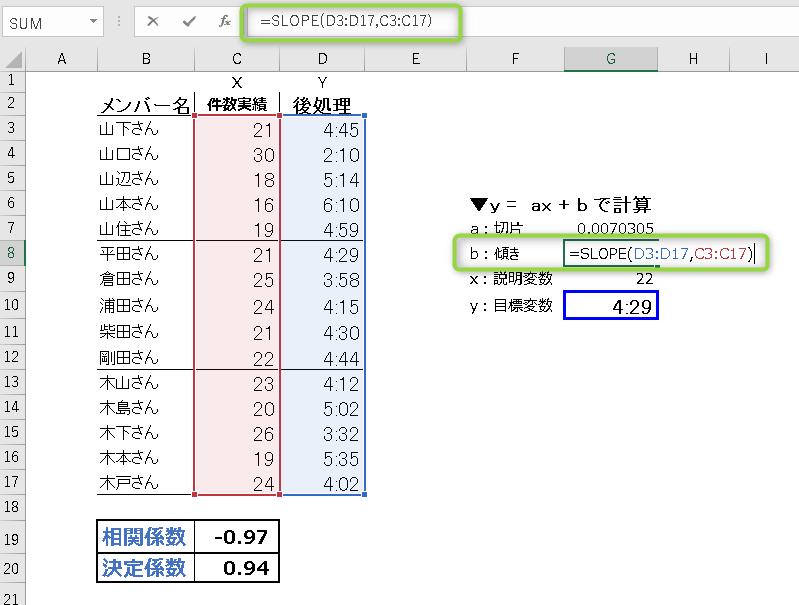
- STEP4
セルG9の説明変数には、応答目標である「22」を入れます。
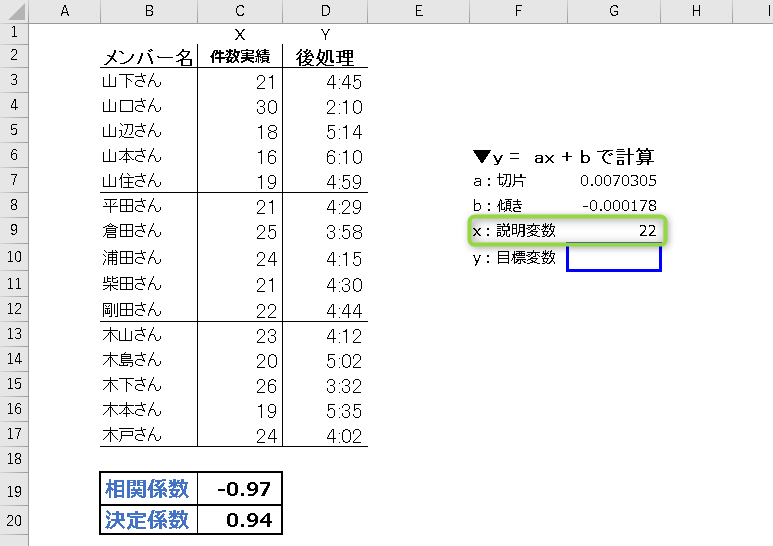
- STEP5
セルG10に回帰分析の計算式通り入力します。
=G7+(G8*G9)
y:目標変数 = (a:切片 × X:説明変数)+b:傾き
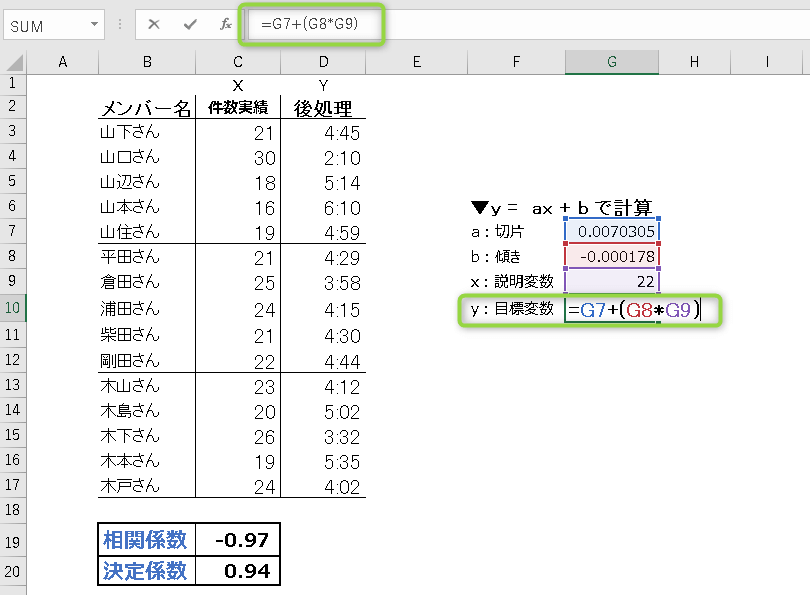
- STEP6
計算終了です。
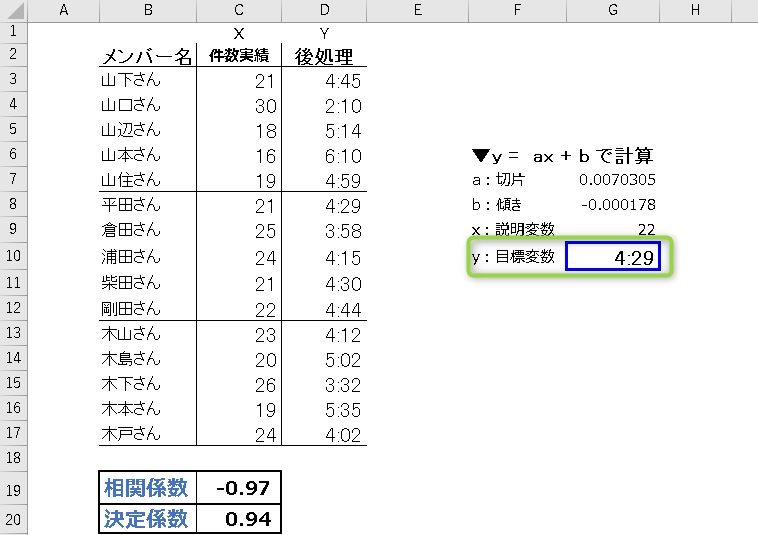
この結果、以下であると言えます。
「応答件数22件の時、後処理が4:29だ」
FORECAST関数で計算する方法と同じ結果が出ました。
以上
まとめ:コールセンターは数字が命!単回帰でスマートに報告を


上司さん、
後処理を4分29秒以内なら、
応答件数22件まで伸びることが分かりました。

確認ありがとう!
では、その時間を上回っているメンバーをしっかりフォローよろしくね!

承知しましたー!
他の分析手法の紹介記事はこちら
コールセンター運営に必要な分析方法を図解でまとめました。
これで数字に強い管理者間違いなし!です。
コールセンターで予測を立てるのに参考にした書籍

日々のコールセンター業務で、予測を立てなければならないこと、多いと思います。
以下は私が根拠ある予測を立てたいとき、参考にした本です。
孫社長にたたきこまれた すごい「数値化」仕事術
コンタクトセンター スーパーバイザー 完全マニュアル
本を読む時間がない人向けサービス

- 現場のレベルについけない
- ライバルと差をつけたい
- 分からないことが分からない
などの悩みを放置していませんか?
変化の激しいコールセンターで取り残されると「いつでも替えの利く人材」に…。
私は過去、ライバルには勝ちたいものの、何を学ぶべきかも分からない残念な管理者でした。
そこから私が長い期間をかけて探し出し、使ってみて納得した学習コンテンツをまとめています。
どれも読書と同等かそれ以上の効率的な学び方です。
将来のための自己投資を始めましょう。
本の要約サイト「flier」。

1冊10分で読めるビジネス本の要約サイト「flier」。
» 参考:【7日間無料】flier(フライヤー)は今おすすめ!お試しキャンペーン有
ビジネスパーソンが今読むべき本を厳選。
月単位でのサブスクタイプですが、7日間は無料体験キャンペーン実施中。

私はシルバープランで使い続けてます!
Udemy(ユーデミー)

世界最大級のオンライン学習プラットフォーム。
受講者数は2019年時点で約3,000万人。
Excelの使い方、プレゼン方法、クレーム対応の基礎など幅広い知識を集中的に学べます。
» 参考:Udemyをおすすめ出来る理由【動画学習という近道】

ビジネスパーソン向けのコンテンツが豊富!
最後までお読みいただき、
ありがとうございます。
このサイトでは
コールセンターという仕事をどうハックするか、
私個人が学んだことを発信してます。

是非トップページをお気に入り登録お願いします!
更新情報はSNSでも発信中です。




コメント